Imagine showing up to a project where the whole team was filled with joy, like a well-choreographed Broadway musical, where everyone dances and sings even under the direst of circumstances. It would be like releasing a barrel of monkeys — as the saying goes. Probably not the ideal environment for design and construction of complex spaces. Or is it? What is wrong with enjoying what we do — working together and teaching others? I think we all have a lifetime of improvements to focus on in our given trades. I’m not about to learn how to do a bell kick or publicly display a bass vibrato while singing, “Saaaanitary; where the waste goes flowing down the drain,” but I can keep an open mind and look for ways to hone my trade.
One of the unique things about what we do is that we form “temporary social networks” in order to construct projects. These networks usually consist of designers, engineers, project managers, owners, architects and contractors. Sometimes, these projects are small renovations that may take only months to design and build. Other times, these projects go on for many years. Most of us would probably agree that the more quickly we can build trust with one another, the more we can work together and, dare I say, “enjoy” our work.
One of the first formulas I ever learned related to plumbing engineering was the flow rate through a fixture drain, outlined in the Volume 1 of the “ASPE Plumbing Engineers Design Handbook (PEDH).” The equation is elegant in its simplicity, as it describes flow through an opening with water under the pressure of gravitational head.
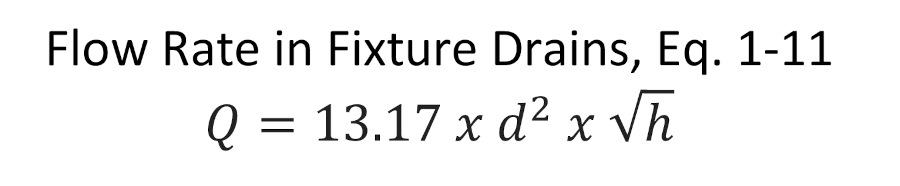
Where Q is the flow rate in gallons per minute (gpm), d is the orifice diameter in inches and h is the mean vertical height about the outlet in feet. The great thing about this formula is somebody took the time to distill Bernoulli’s equation down to a practical equation in units we use every day. The reason we would use mean, or average height, is because the flow rate will decrease as the water level decreases.
Practical application
Putting this to practical use, let us say our barrel of monkeys was actually a rain barrel of monkeys (filled with rainwater naturally), and we want to fill our watering can through a 1/2-inch spigot down near the bottom of the barrel. How long would it take to fill our 1 gallon watering can? Rain barrels are around 3 feet in height, and it is recommended to raise them a couple feet in order to get good drainage.
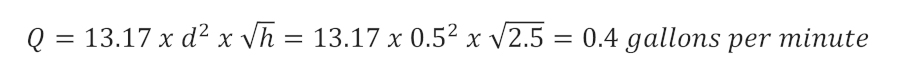
It would take about two and a half minutes, or 150 seconds, to fill our 1 gallon water can. Some rain barrel experts recommend installing the rain barrel even higher off the ground if possible. How much would raising it 15 feet increase the flow rate? I’ll use a mean height of 9 feet for this example (15 feet + 3 feet, divided in half).
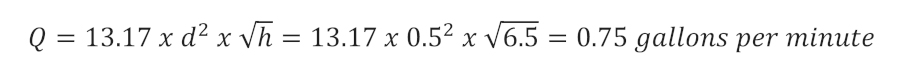
We may have known intuitively that the taller a column of water is, the faster it flows through a pipe or outlet. Now we know there is an equation to describe this phenomena, and we can use it to design and engineer systems.
One of the most practical applications for this is “drain down” from a 3-pot sink. The state code I am most familiar with requires us to calculate the capacity of the sink, and then size the grease interceptor appropriately. Many interceptors have a flow control device that limits the flow through the device. The idea of sizing an interceptor for a 3-pot kitchen sink is understanding that the user could fill all three bays with water to soak kettles and cook pans. Once the person washing dishes is ready to clean the pots and pans, they could drain all 3 bays at the same time. Let’s look at a 48” long by 24” wide sink with a quantity of (3) 12-inch deep bays. The total volume of these sinks is calculated as follows:
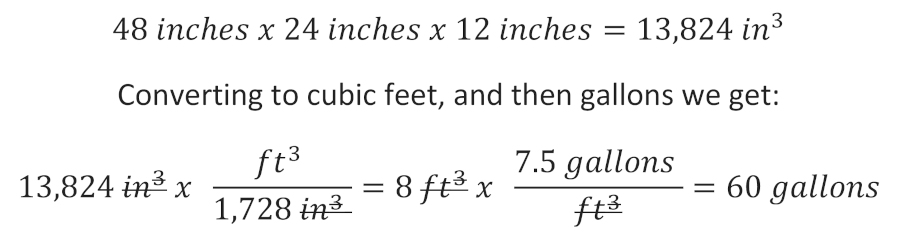
The code we use allows a drainage load of 75%, which takes into practical consideration that the capacity of the sink will not be filled to the brim, and that scullery will displace some of the hot greasy water. Applying a drainage load of 75% to the total capacity of 60 gallons gives us an actual drainage load of 45 gallons. The recommended drain down is 1 to 2 minutes, which would require us to size a grease interceptor that can handle 45 to 22.5 gpm.
What if, in fact, there were no flow control devices and we allowed open flow through our 3 inch waste pipe? We can determine the flow rate by applying equation 1-11; Flow Rate in Fixture Drains. For the equation below, I’ll use a mean depth of 1.5 feet. This will be the average sink depth to the outlet of the waste pipe.
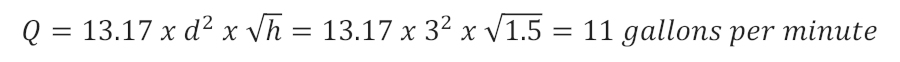
What is interesting about our result is the flow rate is much lower than we would typically use to size a grease interceptor. This is a good example of applying plumbing engineering principles to our design. What would an inspector think?
If you enjoy applying the equations and mathematics that are presented to us, chances are you are in the right field. Even if you do not get to practice them every day, familiarize yourself with the equations and learn something new when you have a chance. Somehow, between the time you punch in and punch out for work, I hope you find joy in what you do.



