ditor’s note: This is the fourth in a series of stories that borrows from daily life experiences to illustrate engineering concepts.

I recently spoke with a civil engineer who had an electrical engineering design challenge. Who better to ask than someone with experience in plumbing engineering?

Sounds like the introduction to a bad engineering joke. Naturally, I went straight to the ASPE design handbooks and my “Mechanical Engineering Reference Manual” for a solution.

The design challenge he presented was this: During the summer months in the Southwest desert, how close to the ground will high-tension electrical wires come to the ground if they were installed during the winter? He informed me that there was a code requirement that the wires should not “sag” to within 25 feet of the ground. The wires could be aluminum or copper, and they were supported by structures that were installed 1/8-mile apart.

The gears in my head turned slowly, activating a chain lift that raised an old vault door where some equations were kept.

The first equation that came to my mind was from the “ASPE Design Manual, Volume 4.” Equation 11-1 helps us determine the expansion of piping due to changes in temperature. In plumbing and hydronics, piping will expand as the fluid inside changes temperature. This is important for us to know so that we include design elements that accommodate this expansion or contraction.

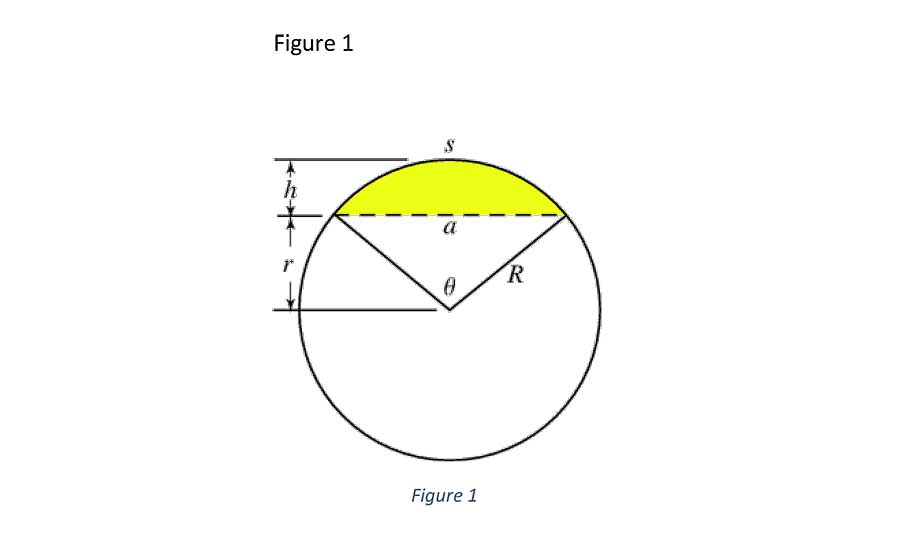
> FIGURE 1.

Common design elements include expansions loops and expansion tanks. There are very good reasons for us to consider these types of physical phenomena. I think a lot of it boils down to learning from others who “learned the hard way.”

The rest of the story

The second part of the equation that I wanted to determine was the installed length of high- tension wire. It would be an arc, whose “chord” was 1/8-mile long. I was fairly comfortable with geometry and I had a strong hunch that there were mathematical formulas that helped determine all the bits and pieces of circles and triangles.

The “Mechanical Engineering Reference Manual” has a whole appendix related to this, and it falls under the topic of Mensuration, defined as “the measuring of geometric magnitudes, lengths, areas and volumes.” Once I determined the length of wire, I could make some assumptions and figure out if the wire would sag down far enough in the summer to clothesline some unsuspecting ATV enthusiast enjoying the desert trails.

We can see from Figure 1 above that “h” is the distance that the high-tension wire would sag and “s” is the length of wire between supports. I did some research and found out that 5% is the maximum nominal tolerance for a high-tension wire to sag. Since 660 feet is 1/8 of a mile, I calculated the maximum sag, “h”, to be 33 feet.  The equation I used out of the mensuration figures in MERM to find the length of the arc is:

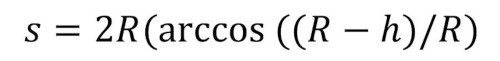
It turns out that the total length of the high-tension wire, installed at 35°F during the desert winter is 663 feet.

Next, I took this length of wire and plugged it into the equation for expansion of a material due to change in temperature,  Performing this analysis for both copper and aluminum materials during a hot summer day of 125°F, resulted in a total expansion of 12 inches and 17 inches respectively. I then plugged this extended length back into the mensuration formulas to find out the additional “sag.” See Table 1 on Page 22.

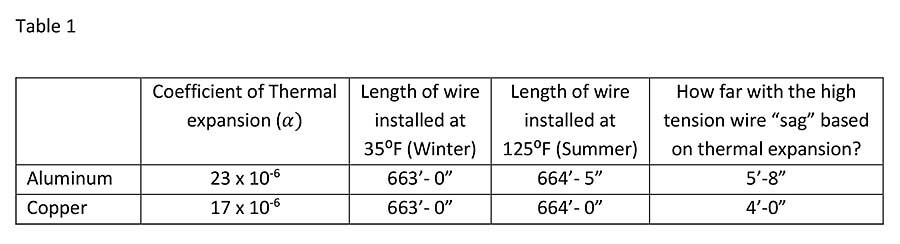
> TABLE 1.

What I’ve tried to present for you is a design problem where you can use the art of engineering. Problems like this come up now and then and I think it’s what makes our jobs interesting. Interesting is probably not the proper term when you find out that the high-tension wire did indeed “sag” below the code-required 25-foot height above grade after it was installed.

The art of our practice comes with the idea that we can apply what we know to a variety of design challenges. If we practice staying curious about different things, we will be prepared to work together and figure things out as they come up.

One of the funniest things I learned from this design problem: There is real mathematical term for that distance between the chord of a circle and the arc radius. It’s actually called the “sagitta.”