We all have certain skills we’ve practiced over time that become like second nature. Those skills might involve a hobby we’ve gotten good at or an aptitude we have a proclivity towards; things that come natural to us. With our careers, these skills could encompass the things we do day in and day out, such as sweating pipe or calculating pipe sizes.
Earlier in my career, I worked for a manufacturer’s representative that distributed pumps. For years, I answered the phone and talked to people about pumps — centrifugal, gear, diaphragm, progressive cavity, vertical turbine, self-priming — the list goes on and on. Nowadays, if a pump sizing application comes up, I jump right on it. For me, it’s like riding a bike.
When you stop and think about it, understanding a centrifugal pump is just like riding a bicycle. Anyone who has ever ridden a “derailleur” knows that you shift gears to maximize your pedaling efficiency. You want to pedal with just the right amount of resistance to operate your 10-speed in that “sweet spot.” If your gears are set too low on a flat stretch, it might feel like you are freewheeling and your legs can’t keep up with the pedals. This is an undesirable condition. It’s a situation where your legs are moving much more than they need to. The analogy to a centrifugal pump is called “run-out.” Try to go up a hill in high gear and you could “dead head.” Sizing a pump involves knowing what type of terrain you are going to ride on and picking the correct gear. The Affinity Laws help us do that.
Understanding sizing
The Affinity Laws are important laws to understand for sizing centrifugal pumps, the kind of pumps we use in plumbing systems for pressure boosting, wastewater ejectors and hot water circulation. The term “affinity” in this case is used in the context of one thing being similar to another. These three laws get their origins from mathematical theories related to dimensional analysis and similitude. It’s almost as simple as saying, “If pump B is twice as big as pump A, it will pump twice as much fluid.”
When you look up the Affinity Laws in the ASPE Design Handbook Vol. 1, they are broken up into (two) equations; 1-21A and 1-21B. The first describes the relationships based on change in speed and the second outlines them in relation to change in impeller diameter. I’d like to present them below as they relate to proportionality. As you study them, you will realize that there are three characteristics that change proportionally; flow, head and horsepower required.
The first relationship shows us that the flow rate of a centrifugal pump is directly proportional to the impeller size or speed. This reiterates the statement I made above that if the pump is twice as big, it will pump twice as much. Or, looking at our bicycle analogy, if you pedal twice as fast you’ll go twice as far. Pretty simple, right?
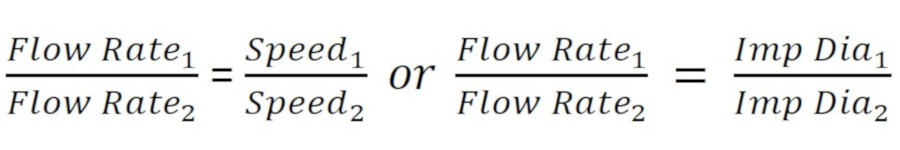
The second relationship is the one that is most useful for getting out of a plumbing engineering bind. This is the reason why we should design with a safety factor and consider specifying pumps with trimmed impellers and size our motors to cover run-out. Total dynamic head changes by the square of the proportion to speed or impeller diameter.
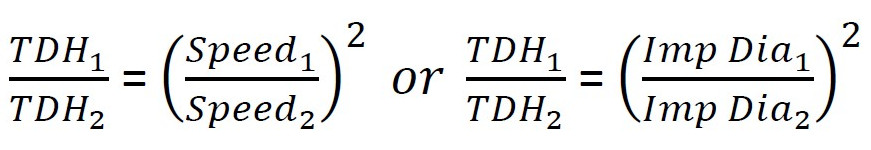
Here’s a scenario: You’ve copied the same ejector pump specification that you’ve used on the last seven jobs from one to another, a tried and true ejector, pumping 20 gpm at 20 feet total dynamic head — just right for picking up a few floor drains and a mop sink in the basement of an office building. Except this time, the pump is located in a parking garage on the side of a hill and the gravity main is 15 feet higher than you thought. When your pump rep helped you out, seven jobs ago, he/she gave you a specification for a pump with a 7-inch volute and 5-inch impeller. “Hmm, I wonder if they might have seen this scenario before?”
The pump, with the 5-inch impeller, has a 25 foot shut off head. Using the affinity laws, we can do a quick ‘back of napkin’ calculation to see if swapping out that impeller could overcome that extra 15 feet in elevation. Here’s the calculation:
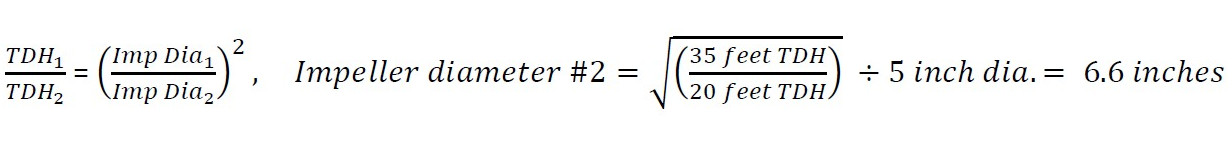
This is great news, right? Maybe we could lessen the cost of fixing the issue by getting the larger impeller from the factory and retrofitting the pump in the field. Before we get too far ahead of ourselves, there is one more Affinity Law we need to check. The horsepower required to operate with the larger impeller will increase by the impeller ratio (or speed ratio) to the power of 3.
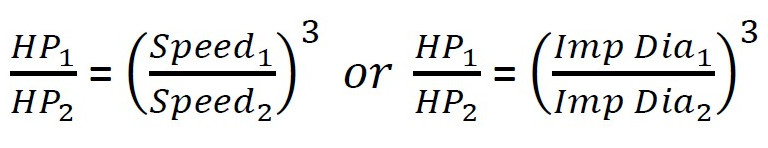
Calculating the theoretical power required for 20 gpm at 20 feet TDH using formula 1-22A in the ASPE Design guide, we get:
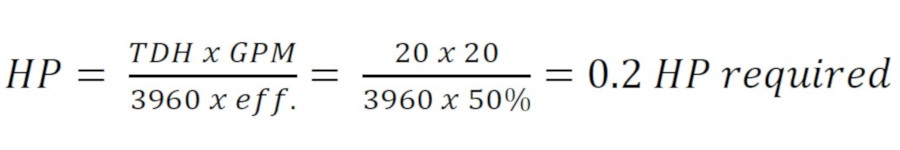
By increasing the impeller diameter from 5 inches to 6.6 inches, the new HP required will be close to half a HP. That is more than double the HP required for a 30% increase in impeller size. When you think about why the power required increases so much, think about riding a stationary bike at the gym. You can ride for a leisurely mile and hardly burn any calories, or go full speed and really work up a sweat. Work is that mile you’ve ridden where power is the rate at which you’ve completed that work.
Life is a lot like pump laws; follow your instincts and learn about the things that you have an affinity toward. You’ll be surprised to find that you’ve become an expert in the things you work at. Those skills will stay with you, and if life ever knocks you down, you’ll be able to get back up and start where you left off; just like riding a bike.




