Every culture has its own nursery rhymes with which they initiate their young. I grew up with a song called the “Itsy Bitsy Spider,” about a spider that gets flushed out of a rainleader. While singing, the song leader would make hand gestures with their fingers and thumbs, mimicking the actions of a spider fighting against the odds. The spiders experience illuminates a fascinating element of plumbing design: Terminal velocity.

Terminal velocity is the answer to a question all plumbing engineers ask at some point in their careers: What happens as drainage descends down a straight vertical pipe and gets faster and faster? The acceleration due to gravity must eventually cause the water to move so fast that it becomes damaging to the piping system. Let’s look at a hypothetical situation that ignores terminal velocity. 

Do the math

At an acceleration of 32 ft/s², the water would be travelling at 96 ft/s after only 3 seconds. That is pretty fast when you think about it — around 65 mph. If someone flushed a toilet in a high-rise penthouse, 75 feet above the lowest fire department vehicular access, it would only take 2.16 seconds for that slug of water to reach the bottom of the stack. 

The force from the hypothetical situation above could be calculated as such: We could even calculate the force that a single flush from the toilet would hit the bottom of the stack with. A low flush, high-efficiency toilet would deliver 0.9 gallons of water. At 8.3 pounds per gallon of water, a single low flush would weigh approximately:

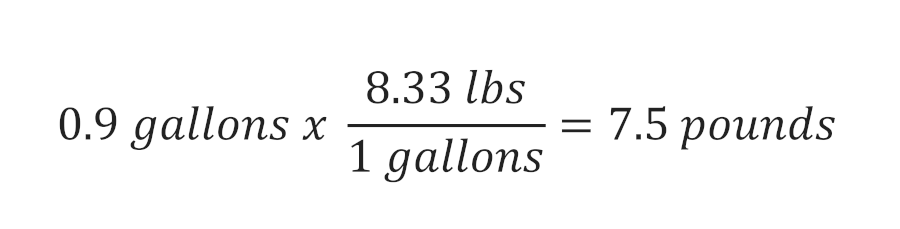
The way we are analyzing this hypothetical situation is by neglecting drag force, which is what will eventually slow down our falling water and cause a maximum terminal velocity. In the absence of drag force, all of the potential energy at the top of the sanitary stack is turned to kinetic energy:

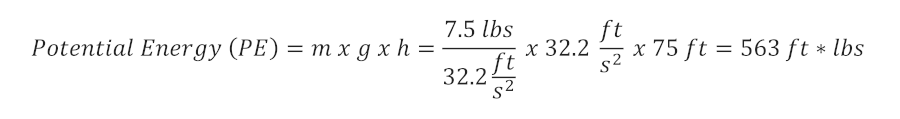
You may have noticed that we divided the 7.5 pounds weight by 32.2 ft/s² . This is necessary when using Imperial units in order to get the mass in units of slugs. The slug is defined as the mass that is accelerated by 1 ft/s² when a force of one pound (lbs) is exerted on it. For our example, the singular flush has a mass of about a quarter slug.

Now, let’s see what really happens as drag and friction forces act on the falling sanitary flow. Terminal velocity is defined as the constant speed that a freely falling object eventually reaches when the resistance of the medium through which it is falling prevents further acceleration. The truth of the matter is that objects don’t just keep speeding up infinitely. They reach a maximum velocity and maintain that throughout their descent.

Volume one of the “ASPE Plumbing Engineering Design Handbook,” gives us a formula to use to help determine terminal velocity. Equation 1-10A reads:

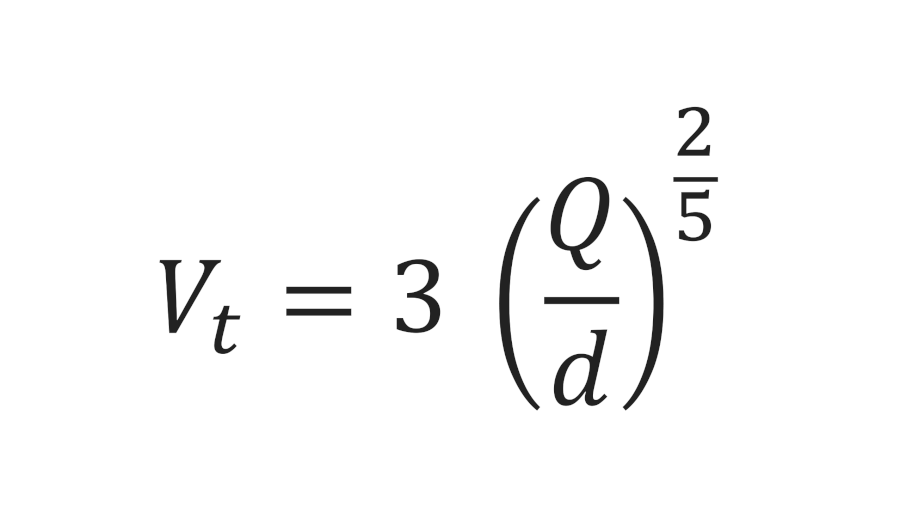
Where “Q” is flow in gpm and “d” is the stack diameter in inches. I’m sure that there is empirical testing to show the actual flow rate from a water closet. I think of it this way: If it takes 2 seconds for a toilet to flush 0.9 gallons, then that translates to 27 gpm. Assuming a 4-inch sanitary stack, our terminal velocity equates to:

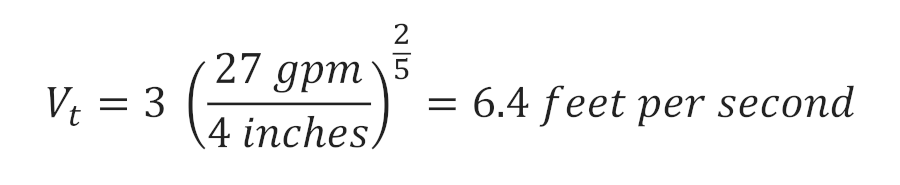
6.4 ft/s is a much more realistic speed than the 96 ft/s we calculated earlier. Where our water was previously falling at around highway speed, drag and friction forces have slowed us down to a slow roll of about 4.5 mph, above scouring velocity for drainage flow through a gravity pipe.

Terminal velocity of falling objects through fluids (such as air) can be determined by using other methods outlined in the topic of fluid dynamics. A great resource for these formulas and examples is the “Mechanical Engineering Resource Manual,” sometimes referred to simply as MERM. These analyses can get quite interesting as you evaluate the shape of objects and their drag coefficients.

As far as plumbing engineering is concerned, there is much more to consider when designing tall sanitary and storm stacks. The second volume of the “ASPE Plumbing Engineering Design Handbook,” discusses the effects of flow and venting, hydraulic jump and stack offsets. These are all important factors to consider. Hydraulic jump occurs due to the transition from vertical to horizontal flow. A reduction in velocity occurs causing a cresting flowing fluid. I imagine this as the same affect you get when you take a flume ride at the amusement park and there is that large splash that dissipates the energy from the gut churning slide.

The energy we feel in our gut when we go down a flume slide is that conservation of potential to kinetic energy and thanks to terminal velocity it has a limit. It does not exceed more than we can handle. We can design plumbing systems with confidence when we understand terminal velocity and the effects of proper venting and stack offsets.

In a strange way, maybe the “Itsy Bitsy Spider” understands terminal velocity, or it would not decide to build its web at the base of a rain leader. For those who know the song, it is worth noting that it has a happy ending: “Out came the sun and dried up all the rain, and the itsy bitsy spider climbed up the spout again.” If it feels like life is coming at you too fast, try to assure yourself that just like terminal velocity, there is a limit to how much we can take. There may be a bump at the end of the drop, but things have a way of smoothing out and finding that steady flow.