“Drain carry” is a catchy term for the more technical phrase “The Drainline Transport of Solid Waste in Buildings.” Plumbing contractors and drain-line specialists will understand the challenges associated with clogged drains better than anyone since they are the ones who get the calls and see what gets put down the drain. Plumbing engineers may not always understand the implications of a design if they strictly adhere to the code, especially if they are under pressure to use low-flow fixtures for conservation measures.

As a foundation for public health, plumbing codes outline basic principles that public health is achieved “through properly designed, acceptably installed, and adequately maintained plumbing systems.” Plumbing systems should “… be installed, designed, arranged, constructed and maintained to protect against fouling, deposit of solids, and stoppages.”

Plumbing codes provide guidelines on sanitary pipe sizing per drainage fixture unit and required slope. A commonly held tenet of plumbing design is that 2 feet per second is the minimum velocity required to provide scouring action, also known as self-scouring velocity. This velocity will minimize the settling of solids. How do we determine whether our design achieves that minimum scouring velocity?

For this article, we will be looking at flow in sanitary systems, specifically from water closets. Two questions come to mind: How do we compute the velocity coming out of a water closet? And how do we account for the types of solids that may be introduced into the drain? For the first question, we can apply theoretical formulas based on varying assumptions. The second question may require experimentation and the expertise of those who witness firsthand what clogs sanitary drains. Answering the second question is highly un-predictive as it must consider human behavior.  

The formula that Plumbing Engineers use to calculate velocity of uniform flow in a sloping pipe is called the Manning formula. Uniform flow in a sloped drainage pipe is similar to open channel flow and is mainly dependent upon the height of the water in the pipe and the slope of the pipe.

The formula is:

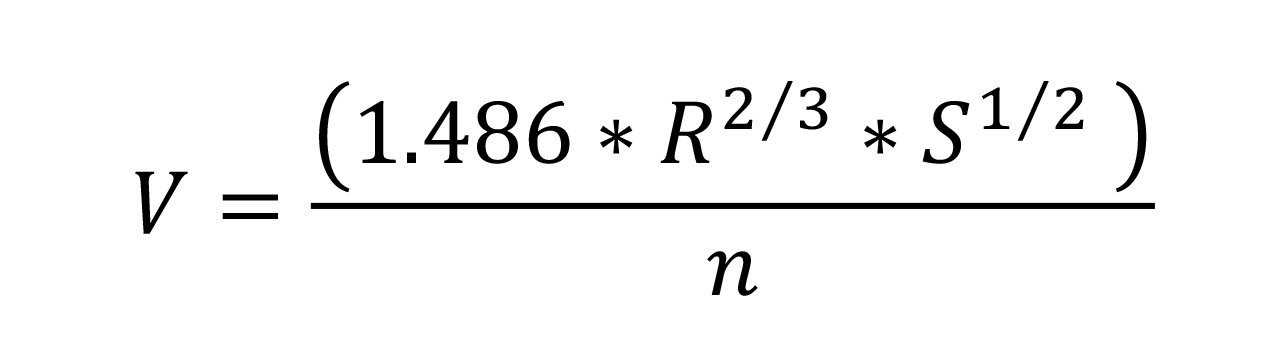
Where velocity is dependent upon the hydraulic radius to the 2/3 power times the square of the slope times 1.486 all divided by the pipe roughness. One of the most interesting factors in this formula is that the velocity does not increase drastically once the pipe is flowing greater than half full. So, what happens with uniform flow up to the pipe being half full, and how do we determine how full the pipe is? I would start with converting flush rate to flow rate. Assuming a best-case scenario of toilet bowl evacuation in 4 seconds. That translates to a flow rate of:

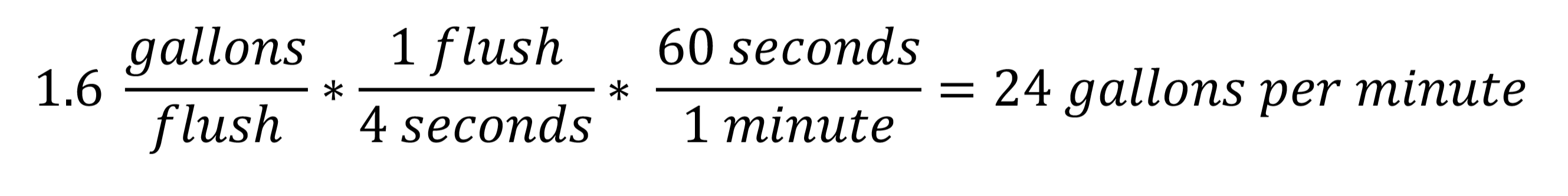
Looking at tables and formulas, 24 gpm flowing through a 4-inch pipe at 1/8 inch per foot slope corresponds to being 35% full, whereas the pipe would be 55% full flowing 24 gpm through a 3-inch pipe. Furthermore, according to the Manning formula, either of these scenarios would produce the same flow velocity of 2 feet per second, just the minimum allowed per code. Let’s take a look at lower flow water closets at 1.28 gallons per flush. The corresponding flow rate would be:

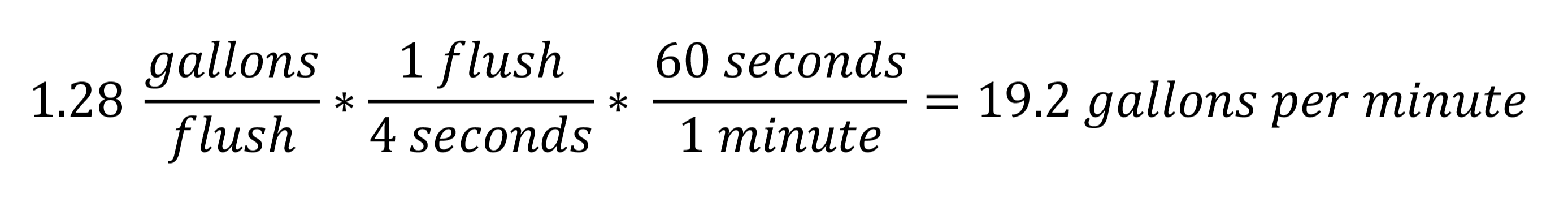
At this flow rate, and with a pipe sloped at 1/8 per foot, neither a 3-inch or 4-inch pipe would meet the required scouring velocity of 2 feet per second. The 3-inch pipe will actually perform better because the hydraulic radius is greater, and the pipe would be flowing closer to half full. This is something to consider as we commonly design systems using 4-inch drainage pipe. I’ll be the first to admit that many times I’ve designed with a larger pipe to achieve a higher invert.

The other variable worth looking at more closely in the Manning formula is S, or slope. What happens when we change the slope from 1/8-inch per foot to 1/4-inch per foot? We can put the 2 scenarios on top of one another and cancel out all of the like terms to get:

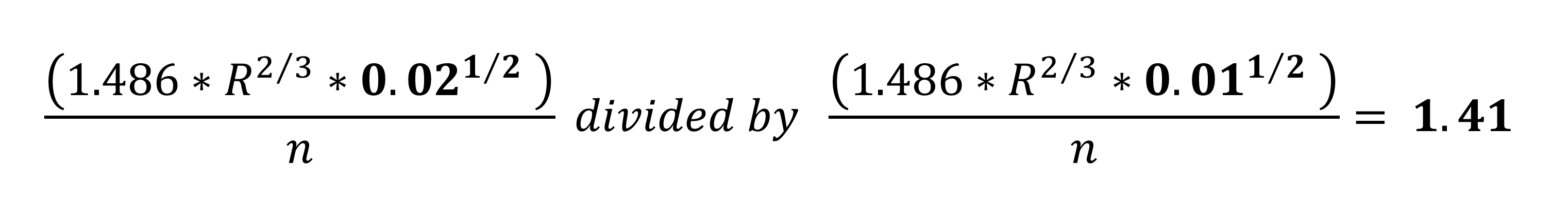
What this tells us is that velocity will increase by a factor of 1.41 when we increase the uniform slope from 1/8-inch to 1/4-inch per foot, regardless of pipe size. Slope has a greater effect on achieving the minimum scouring velocity than the effect of changing the wetted area. I’m guessing that those of you in the field are shaking your heads right now, thinking, “Yeah, we already knew that.”

This brings us to our second question: How do we account for the solids that are introduced into the drain? Think about it: Up to this point, we have looked at the simple flow of water in a sloped pipe (and it isn’t that simple). Once you add the variable of solid waste and toilet paper the results require investigation and experimentation. Credit where credit’s due to organizations such as the Plumbing Engineering Research Coalition (PERC), formed in 2009, who performed the scientific testing to determine which factors had the greatest effect on our plumbing systems. I would encourage you to look up their findings.

As plumbing engineers, we don’t have control over what gets flushed down the drain but we do have some control over what we design and what’s gets built for our clients. It is important that we understand the factors that go into our designs, including experimental research by organizations like PERC. Also, it is important to know that sometimes the code minimum might contradict certain design standards. On top of how we design, don’t be hesitant to add a safety factor. This is common practice for many engineered systems that helps account for variations in materials and installation.