
Propylene glycol has been widely accepted and utilized in fire sprinkler systems for many years. Until recently it has been restricted to antifreeze loops on wet pipe sprinkler systems. Innovative advances in the design of sprinkler systems and full-scale fire testing of class 2 commodities in rack storage configurations have demonstrated that sprinkler systems pre-primed with a water and propylene glycol solution utilizing K 25.2 sprinklers are a viable option for the protection of cold storage occupancies under certain conditions.
Full-scale burn testing has been conducted utilizing specific types of sprinkler systems, propylene glycol solutions and K 25.2 ESFR sprinklers that have been specifically tested for the application. The listings and manufacturer's installation instructions for these propylene glycol systems are very specific with regards to the type of system, the system volume and the piping configuration. If a system is selected to protect a cold storage occupancy using a propylene glycol solution, the fire protection designer must verify the appropriate product listings. In addition, the manufacturer's technical literature must be reviewed to ensure that the system design is in compliance with the listings and that all of the required components have been installed.
Application
There are currently two sprinkler system configurations utilized for installation in cold storage applications that include piping pre-primed with the propylene glycol solution. The early versions of these systems were wet pipe sprinkler systems. However, through improvements and modifications implemented to enhance system performance in cold storage environments, the optimal system has evolved into a single interlock preaction system pre-primed with propylene glycol solution rather than pressurized air. In both cases, these systems are used in conjunction with K 25.2 sprinklers that have been specifically tested for the application. K 25.2 sprinklers allow the designer more flexibility in the design and may allow the in-rack sprinklers required for the rack storage to be removed. In either case, a 50% or 35% propylene glycol and water solution will be used, depending on what the minimum temperature is expected to be in the cold storage environment.In addition to evaluating manufacturer's recommendations and the specific equipment required for these special sprinkler systems, the designer must approach the hydraulic calculation with the understanding that a liquid (other than water) will initially be moving through the piping network. Traditionally, when the fire protection designer is performing the hydraulic calculation for a sprinkler system in accordance with NFPA 13, the Hazen-Williams formula for determining the friction loss is adequate. However, because the propylene glycol solution is a much more viscous liquid than water, the system volumes are much larger than a traditional antifreeze loop, and the cold storage environment may experience sustained temperatures as low as -20°F, the Darcy-Weisbach formula must be used in one of the two required hydraulic calculations for systems utilizing propylene glycol solution.
The Darcy-Weisbach formula for calculating friction loss is more accurate than Hazen-Williams for determining friction loss in piping in several situations encountered in sprinkler system design, including the calculations for foam concentrate (not solution) piping, high water velocities such as those in water mist systems, and the friction loss calculations for antifreeze systems, especially when these systems have a large volume and are in areas with very low temperatures, such as cold storage areas. The primary reason for this is that the Hazen-Williams formula does not allow the user to take into account a change in the viscosity of a liquid being calculated. The Darcy-Weisbach formula does allow the user to modify the viscosity of liquid being calculated when determining a part of the equation called the Reynolds Number, which we will define later in the article.
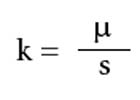
Viscosity
Crane's Technical Paper No. 410, "Flow of Fluids Through Valves, Fittings and Pipe,"Where:
k = kinematic viscosity
μ = dynamic viscosity
s = specific gravity of the liquid
The unit for kinematic viscosity is called a stoke, where one stoke is equal to 100 centistokes. The designer of the system must determine which way the viscosity units (dynamic or kinematic) have been provided by the antifreeze manufacturer to ensure the Darcy-Weisbach formula is performed properly. The example provided here will use the dynamic viscosity units-poise.
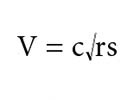
Formula History
To gain an understanding of exactly where the differences lie within Hazen-Williams and Darcy-Weisbach, it is important to understand the history of each formula and the factors each of them take into consideration when calculating friction loss. As described by Harold Wass inSprinkler Hydraulics, each formula was actually derived and uses the fundamental concepts developed by the French engineer Antoine de Chezy. In Chezy's formula, friction loss is calculated by using a coefficient reflecting the roughness of the pipe, the internal hydraulic radius of the pipe and the hydraulic slope, which is the friction loss per unit length of pipe. The formula is expressed as: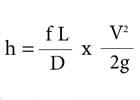
c = coefficient for pipe roughness
r = internal hydraulic radius
s = the hydraulic slope or friction loss per length unit
This formula was refined further by several engineers, including Henri Darcy and Julius Weisbach, into what is referred to today as the Darcy-Weisbach formula. The Darcy-Weisbach formula expands on the concept of the friction factor first utilized by Chezy and modifies the formula into:
Where:
h = friction loss (ft of head)
f = friction loss factor (from Moody Diagram)
L = length of pipe or tube (ft)
V = velocity of flow in tube (ft/sec)
D = diameter of pipe (ft)
g = gravitational constant of 32.2 ft/sec
To the experienced fire protection designer, most of the information required to complete the calculation in the Darcy-Weisbach formula is familiar and self-explanatory. However, as we stated above, the formula has expanded on the concept of the friction factor (f). The friction factor is determined by using what is called the "Moody Chart."
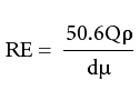
Reynolds Number
The "Moody Chart"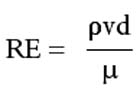
Q = flow (gpm)
d = internal pipe diameter (in.)
r = weight density of fluid
μ = dynamic (absolute) viscosity
Or by using:
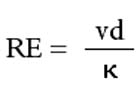
r = density
v = velocity
d = internal pipe diameter (feet)
μ = dynamic (absolute) viscosity
If the kinematic viscosity is provided, the Reynolds number may be determined by using:
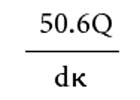
Where:
v = velocity
d = internal pipe diameter (feet)
k = kinematic viscosity
When using any of the above methods for determining the Reynolds Number, the viscosity of liquid is used. Depending on the temperature of the cold storage environment, the viscosity of the propylene glycol solution is going to change. The dynamic (absolute) viscosity of propylene glycol solution at 60°F is 8.13 centipoise and 180 centipoise at -20°F. Given the large change in viscosity, it can be anticipated that the friction factor determined on the "Moody Chart"
Example
If we use the Darcy-Weisbach formula to calculate the friction loss for 400 gallons of propylene glycol with a 50% solution flowing through 30 feet of 2.5-inch Schedule 40 steel pipe at 60°F and then again at -20°F, let's analyze the results.Using the above parameters at 60°, the friction loss is calculated at approximately 16 psi over the 30 feet of pipe. Using the exact parameters above but adjusting the viscosity units for the decrease in temperature to -20°, the friction loss is calculated at approximately 31 psi for the 30 feet of pipe. As you can see, there is a 15 psi difference; if the fire protection designer did not account for the difference in the liquid's viscosity, the calculation of friction loss would have been corrupted.
Hazen-Williams
In the early 1900s, Gardner Williams and Allan Hazen again modified the Chezy formula into the Hazen-Williams formula as we know it today. As with the Darcy-Weisbach formula, the internal roughness of the piping, flow of water, velocity and hydraulic slope are taken into consideration during the calculation of friction loss. However, the Hazen-Williams formula was not revised to take into consideration different viscosities of liquids like the Darcy-Weisbach formula does during the calculation of the Reynolds Number. Instead the Hazen-Williams formula uses a pipe roughness coefficient called the "C"Conclusion
Regardless of which formula is being used, the purpose of applying a friction loss formula is to ensure that sprinkler system design has properly accounted for the loss of pressure within the flowing water or water antifreeze solution due to friction with the internal pipe wall. Because fire protection hydraulics is only concerned with a few basic elements in the flow computations, additional steps must be taken for a fluid other than water.
Historically, as Harry Hickey describes in "Hydraulics for Fire Protection,"