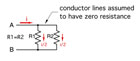
Figure 1.

In many hydronic systems, there’s a need to divide system flow into several equal streams that pass through several identical components. The physics necessary for this are simple: If the flow resistance of each parallel path is the same, the total flow will divide equally. It’s the same concept at work in the electrical circuit shown in Figure 1.

If resistances R1 and R2 are equal, the electrical current through point A will split into equal branch currents passing through R1 and R2. Similar results occur regardless of the number of branches, as long as all branch resistances are equal (e.g., four equal branch resistances will each get 1/4 of the total current flow).

The lines connecting components together in electrical schematics are assumed to have zero resistance. This, of course, is impossible for any real conductor, but when the lines represent very-low-resistance conductors, it’s a reasonable approximation that simplifies circuit analysis.

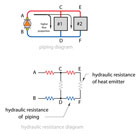
Figure 2.

Figure 2 (on page 27) shows an analogous situation for a hydronic circuit with two parallel branches. The heat emitters and piping in each branch are often identical, and thus, have equal flow resistance. However, unlike the conductors in the electrical schematic, the supply piping from C to E and return piping from F to D may have significant flow resistance.

It’s also apparent that the flow path through heat emitter #2 is longer than that through heat emitter #1. Thus, the flow resistance of path ACEFDB is greater than that of path ACDB. Flows will not divide up equally in such a system. Instead, the branch flows depend on the resistance of the supply and return piping between the branches (e.g., path CE and DF in Figure 2).



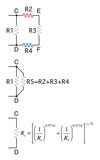
Figure 3.

Branch flows can be calculated by reducing the parallel portion of the resistor network (CEFD) to a single equivalent hydraulic resistance, as shown in Figure 3, and then applying Equations 1 and 2.



Equation 1.

Where:

ƒT = total flow entering node C and leaving node D

ƒ1 = flow through hydraulic resistance R1

R1 = hydraulic resistance through crossover containing heat emitter #1

Re = equivalent hydraulic resistance determined as shown in Figure 3



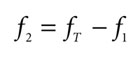
Equation 2.

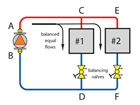
The exponents (1.75 and 0.5714 =1/1.75) are based on the use of smooth tubing in the system. They are based on empirical approximations of the Moody friction factor used in the Darcy Weisbach equation. When steel or iron pipe is used, the theoretical value of these exponents would be 2.0 and 0.5.

Figure 4.

The piping system shown in Figure 2 is called a two-pipe direct return system. If equal flows are required through each branch, it’s necessary to adjust the hydraulic resistance of the lower resistance branch using a balancing valve, as shown in Figure 4.

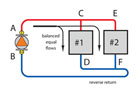
Figure 5.

An alternative piping approach is the reverse return system shown in Figure 5 on page 29. This arrangement has the potential to create approximately equal hydraulic resistance through each crossover, and hence, accomplish equal flow proportions without need for balancing valves.

It’s not wise to assume that every reverse return system will have equal flow proportions through each crossover. Anything that creates a difference in the resistance of the supply or return piping between crossovers will affect these proportions. So would a different type or size of heat emitters in any of the crossovers. A difference in the crossover piping itself (length, type or size) will also change the resistance of that crossover relative to the others and affect flow proportions. For these reasons balancing valves are usually still installed in all the crossovers of reverse return systems, especially large systems with many crossovers or systems that have the potential of being modified over time.

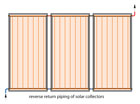
Figure 6.

When Does Reverse Return Make Sense?

Like most concepts in hydronic system design, reverse return has its strengths and limitations. It should not be viewed as one concept that fits all applications.

Reverse return subassemblies make sense when two or more identical devices require equal flow proportions from a common supply. An example would be multiple solar collectors, as shown in Figure 6.

Figure 7.

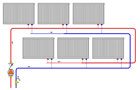
Another situation would be multiple panel radiators serving a common room and controlled by a single zone valve or circulator, as shown in Figure 7.

Reverse return distribution systems make sense when the following conditions are all present:
  • The loads are being supplied from a common circulator
  • The loads served require the same supply temperature
  • The loads served are widely dispersed around the building
  • The distribution piping can make a complete loop around the inside of the building starting and ending in the mechanical room.


Figure 8.

An example is shown in Figure 8 on page 30. Notice that the supply pipe size decreases as the circuit moves away from the mechanical room, while the return pipe size increases. Pipe size changes are made to keep flow velocity along the main approximately equal and in the range of 4 feet per second. They should be made more or less symmetrically to keep pressure drops equal along the supply and return mains.

In systems with relatively short supply and return mains, the designer may elect to use the same pipe size for all mains. This decreases system head loss, which may in turn reduce circulator size. However, it also increases piping cost. A life-cycle cost analysis comparing added hardware cost to reduced operating cost would be the prudent way to evaluate such a tradeoff.

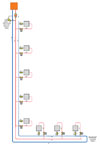
Figure 9.

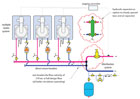
Reverse return piping often doesn’t make sense when the distribution system “dead ends,” as shown in Figure 9 (on page 31). Such an arrangement requires a “third pipe” sized to carry the full system flow from the dead end back to the mechanical room. While this arrangement still provides equal supply temperatures and the “self-balancing” characteristic of the system shown in Figure 7, the third pipe running the entire length of the system adds substantial cost.

Figure 10.

Controlling DP

Although reverse return systems are closer to “self balancing” than direct return systems, they still cause a fixed speed circulator to experience changes in differential pressure due to changes in flow through the crossovers. Such changes, if uncorrected, can cause flow velocities in active crossovers to increase as valves on other crossovers close. This can lead to flow noise, control valve stem lift and erosion corrosion of copper tubing.

One solution is a differential pressure control valve installed across the mains of the system, as shown in Figures 8 and 9. Such valves throttle excess head energy into heat as total system flow drops due to reduced flows in crossovers. Although they accomplish a desired effect (e.g., prevention of excessive differential pressure), they do so in a parasitic manner (e.g., wasting a portion of the head energy of the circulator).

An even better option is a variable-speed distribution circulator programmed to maintain proportional differential pressure control (see “Distribution Efficiency in Hydronic Systems” in June 2006 PME [page 30] for a detailed discussion of this type of differential pressure control). The speed of the circulator automatically adjusts based on the instantaneous flow needs of the distribution system. These “smart” circulators maintain adequate flow while conserving electrical input energy to the pump under partial load conditions. Estimated electrical energy savings from using this approach range from 65% to 80% relative to a fixed-speed wet rotor circulator with PSC motor and equivalent peak performance.

Figure 11.

When It's Not Needed

There are situations where reverse return piping, while possible, does little to improve flow balancing. One example is a multiple boiler system where the boilers are in close proximity and connected to a common header system that has low flow resistance (see Figure 10 on page 31).

Because the pressure drop along the boiler header is so low in comparison to the flow resistance through the boiler heat exchanger, there is virtually no difference in the flow resistance through each boiler path and the point of hydraulic separation. A slight variation in circulator performance could make more difference in flow through a given boiler than the boiler’s position along the short low-resistance direct return headers.

Another situation where reverse return is certainly acceptable but not necessarily required is a typical manifold station for floor-heating circuits (see Figure 10). Again, because the pressure drop along the short manifold is extremely low in comparison to the pressure drop along the floor circuit, the use of reverse return piping will have virtually no effect on individual circuit flows. The larger the bore of the manifold relative to the number of circuits it serves, the less effect reverse return piping has. Also keep in mind that the floor circuits may not all be the same length and hence don’t necessarily need equal flow rates.

Summary

Reverse return piping is an important aspect of hydronic heating technology. Those designing hydronic systems should be familiar with it and know when to apply it, as well as recognize situations where it’s not necessary.