
Issue: 3/05
Plumbing designers are often called upon to design medical gas piping systems, including oxygen, nitrous oxide, nitrogen, carbon dioxide, medical vacuum, WAGD (Waste Anesthetic Gas Disposal) and medical compressed air. As with any gas piping system, in order to determine pipe sizes accurately, we must first determine the maximum anticipated flow. Then, once the flow has been determined, pipe sizes may be selected using standard tables or by direct calculation using various gas-flow formulae.
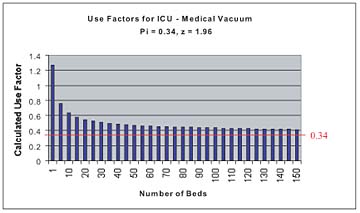
However, calculating medical gas flows and pipe sizes, especially for large facilities such as hospitals, can be a rather complicated process. To determine flow, designers have traditionally counted the number of outlets/inlets served by a section of piping without regard to the location of those outlets/inlets, applied a "use factor"

Medical Gas Demand and Probability
Whenever scientists, engineers and other researchers are called on to calculate certain quantitative information, they often turn to the principles of probability. Probability is a branch of mathematics that is used to determine what is likely to occur (not necessarily what will occur) in a given event or sequence of events. Swiss mathematician Jacob Bernoulli (1654-1705) is credited with the discovery of many of the fundamental principles of probability, including the binomial equation used to generate probability distribution curves, as well as the "Theory of Large Numbers."
The binomial formula (Equation 1) is shown at right.
Equation 1
Where:
P(x) = Probability of getting x positive outcomes
n = number of trials
p = probability of a single trial being successful (e.g., p = 0.5 for Probability of getting a head on a single toss of a coin and p = 1/6 for the probability of getting a two on a single toss of a die, etc.)
x = number of positive outcomes
Equation 1-proven by Jacob Bernoulli in 1685-is used to generate the well-known binomial probability distribution curve, the familiar "bell-shaped"
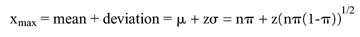

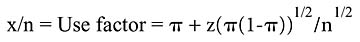

Theory of Large Numbers: A Basis for Determining Probabilities
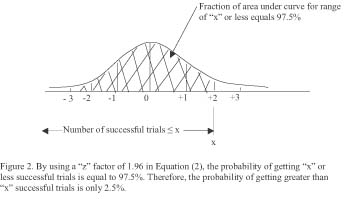
As was pointed out in the examples above, in order to determine the number of positive results that one needs to consider with a stated confidence level, we must not only know the number "n"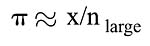
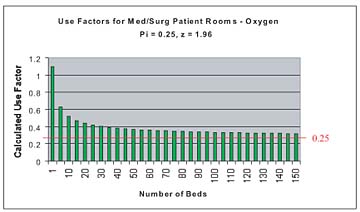
For more information on medical gas pipe sizing, see Part 2 of this article in the April 2005 issue of PME.
